Xoay Ma Trận 90 Độ Python: Thuật Toán In-place Tối Ưu

• Bạn cần xoay ảnh hoặc ma trận dữ liệu nhưng bị giới hạn bộ nhớ (không được tạo mảng mới).

• Nắm vững kỹ thuật Transpose (Chuyển vị) kết hợp Reverse (Đảo ngược) kinh điển trong phỏng vấn Big Tech.

• Giải quyết bài toán này chỉ trong 2 bước logic đơn giản.

Tóm tắt nội dung

• Hiểu rõ yêu cầu “In-place” (Tại chỗ) là gì.

• Công thức toán học: Chuyển vị + Đảo ngược hàng.

• Code Python cơ bản (Vòng lặp lồng).

• Code Python nâng cao (Pythonic one-liner).

• Phân tích Big-O Time & Space.

Bạn xem thêm:

• Giải Thuật Sudoku: Chiến Lược Backtracking Trong Python
• In ma trận xoắn ốc Python: Giải thuật & Code tối ưu
• Thuật Toán Kiểm Tra Sudoku Kích Thước Bất Kỳ

1. Đề bài

Tên bài: Rotate Image (Xoay hình ảnh/ma trận).

Đề bài:

Cho một ma trận vuông kích thước N x N đại diện cho một hình ảnh. Hãy xoay hình ảnh đó 90 độ theo chiều kim đồng hồ.

Yêu cầu bắt buộc: Bạn phải xoay ma trận tại chỗ (in-place), nghĩa là phải sửa đổi trực tiếp trên ma trận đầu vào matrix. Không được cấp phát bộ nhớ cho một ma trận 2 chiều khác để chứa kết quả.

Input:

• Một mảng 2 chiều matrix kích thước N x N.

Output:

• In ra ma trận sau khi xoay (các phần tử cách nhau bởi khoảng trắng).

Constraints:

• 1 <= N <= 1000 (Thực tế Python xử lý tốt, nhưng cần tối ưu).

• -1000 <= matrix[i][j] <= 1000.

Ví dụ 1:

Input:

1 2 3
4 5 6
7 8 9

Output:

7 4 1
8 5 2
9 6 3

Ví dụ 2:

Input:

5 1 9 11
2 4 8 10
13 3 6 7
15 14 12 16

Output:

15 13 2 5
14 3 4 1
12 6 8 9
16 7 10 11

2. Phân tích tư duy

Nếu dùng một ma trận phụ, bài này quá dễ: new_matrix[j][n-1-i] = matrix[i][j]. Nhưng yêu cầu là In-place (Bộ nhớ O(1)).

Chúng ta hãy quan sát sự dịch chuyển của các phần tử trong Ví dụ 1:

• Hàng 1 [1, 2, 3] => trở thành Cột cuối [1, 2, 3] (từ trên xuống).

• Hàng cuối [7, 8, 9] => trở thành Cột đầu [7, 8, 9] (từ trên xuống).

Để thực hiện điều này mà không “xoay vòng” phức tạp từng lớp, ta có một thủ thuật toán học 2 bước:

Bước 1: Transpose (Chuyển vị)

Biến hàng thành cột. Đổi chỗ phần tử matrix[i][j] với matrix[j][i].

Đường chéo chính (1, 5, 9) giữ nguyên.

1 2 3      1 4 7
4 5 6  ->  2 5 8
7 8 9      3 6 9

Bước 2: Reverse Rows (Đảo ngược từng hàng)

Đảo ngược thứ tự các số trong mỗi hàng.

1 4 7      7 4 1
2 5 8  ->  8 5 2
3 6 9      9 6 3  (DONE!)

Tại sao logic này đúng?

• Transpose hoán đổi trục i và j.

• Reverse hoán đổi trục ngang.

• Kết hợp lại tạo ra hiệu ứng xoay 90 độ.

3. Giải pháp 1: 

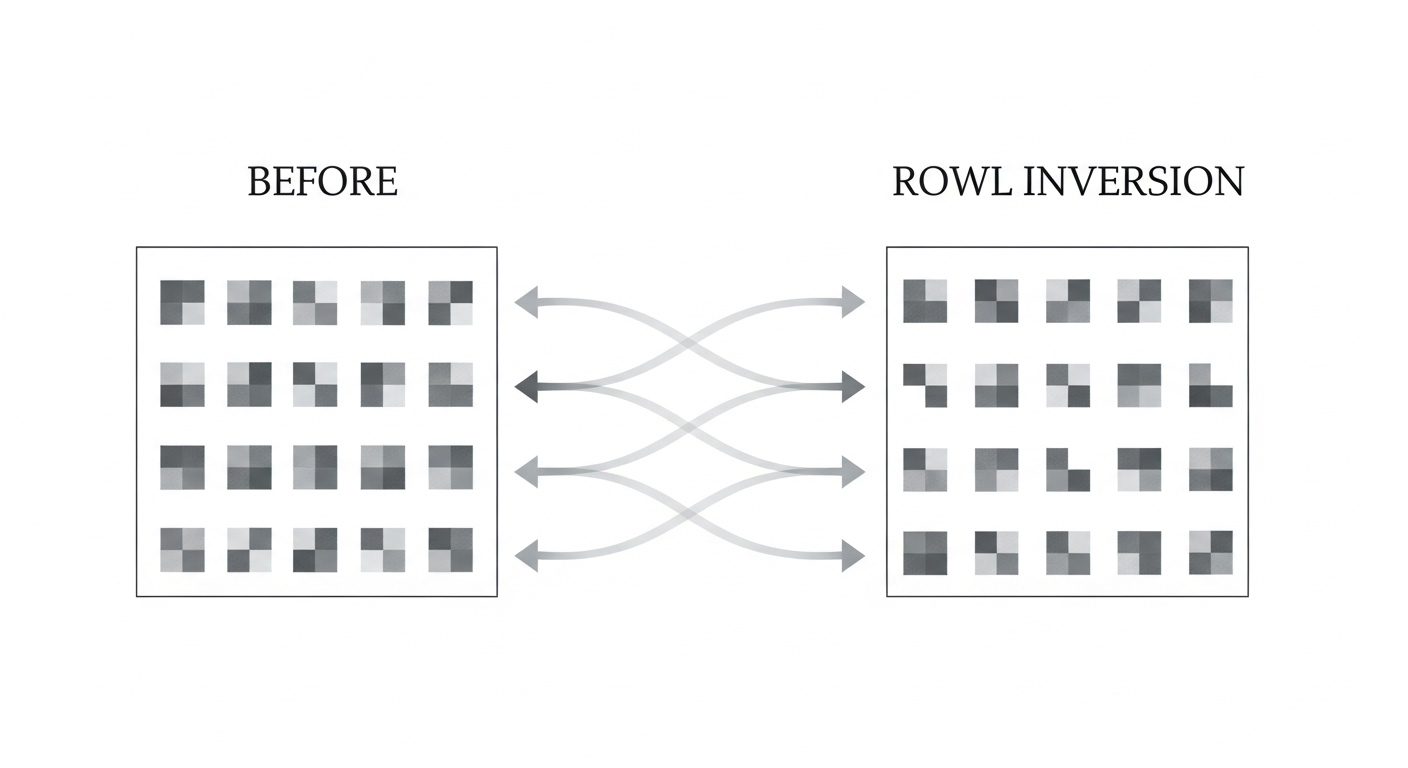
Đây là cách viết code tường minh, sử dụng vòng lặp lồng nhau, thể hiện rõ bạn hiểu cách thao tác chỉ số mảng (index manipulation).

Ý tưởng:

1. Duyệt vòng lặp để thực hiện Transpose (chỉ duyệt tam giác trên để tránh đổi chỗ 2 lần).

2. Duyệt từng hàng để đảo ngược (dùng Two Pointers hoặc hàm có sẵn).

Code Python 

import sys
def print_matrix(matrix):
    for row in matrix:
        print(*row)
def rotate_in_place(matrix):
    n = len(matrix)
    
    # BƯỚC 1: Transpose (Chuyển vị ma trận)
    # Ta chỉ duyệt i từ 0->n và j từ i->n
    # Để tránh việc hoán đổi 2 lần (hoán đổi lại về vị trí cũ)
    for i in range(n):
        for j in range(i + 1, n): # Bắt đầu từ i + 1
            # Swap matrix[i][j] và matrix[j][i]
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
            
    # BƯỚC 2: Reverse từng hàng
    # Có thể dùng vòng lặp hoặc slice của Python
    for i in range(n):
        # Cách thủ công (Two Pointers) để phỏng vấn viên thấy kỹ năng
        left, right = 0, n - 1
        while left < right:
            matrix[i][left], matrix[i][right] = matrix[i][right], matrix[i][left]
            left += 1
            right -= 1
        # Cách Pythonic ngắn gọn hơn: matrix[i].reverse()

# --- Phần đọc Input chuẩn ---
def solve():
    # Đọc input từ stdin
    input_data = sys.stdin.read().split()
    if not input_data:
        return

    # Giả định input vào là một chuỗi các số
    # Bài này thường input dòng đầu là N, hoặc tự suy ra N từ số lượng phần tử
    # Để code linh hoạt, ta đọc n là căn bậc 2 của tổng số phần tử
    
    import math
    total_elements = len(input_data)
    n = int(math.sqrt(total_elements))
    
    if n * n != total_elements:
        # Xử lý trường hợp có thể dòng đầu tiên là N
        # (Tùy đề bài cụ thể, ở đây viết theo format mảng phẳng)
        pass 

    matrix = []
    idx = 0
    for i in range(n):
        row = []
        for j in range(n):
            row.append(int(input_data[idx]))
            idx += 1
        matrix.append(row)

    rotate_in_place(matrix)
    print_matrix(matrix)

if __name__ == "__main__":
    solve()

Phân tích Big-O:

• Time Complexity: O(N^2). Chúng ta duyệt qua toàn bộ các ô của ma trận 2 lần (1 lần transpose, 1 lần reverse). Đây là độ phức tạp tối ưu vì kiểu gì cũng phải chạm vào từng phần tử.

• Space Complexity: O(1). Chúng ta chỉ dùng biến tạm để hoán đổi, không tạo mảng mới.

4. Giải pháp 2: 

Python cung cấp các công cụ cực mạnh như zip và unpacking (*) để xử lý ma trận. Cách này thường dùng trong thực tế (production) hoặc Code Golf, nhưng trong phỏng vấn bạn cần giải thích rõ cơ chế bộ nhớ.

Ý tưởng:

• *matrix: Unpack từng hàng của ma trận.

• zip(*matrix): Gom các phần tử cùng index của các hàng lại với nhau => Tạo ra các cột (chính là Transpose).

• [::-1]: Đảo ngược thứ tự các hàng trước khi zip => Xoay 90 độ.

Code Python

def rotate_pythonic(matrix):
    """
    Giải thích:
    1. matrix[::-1] -> Đảo ngược thứ tự các HÀNG (hàng cuối lên đầu).
    2. *matrix[::-1] -> Tách các hàng ra.
    3. zip(...) -> Gom phần tử thứ 0 của hàng (mới) 0, hàng (mới) 1... 
       => Tạo thành hàng đầu tiên của ma trận kết quả.
    """
    # Lưu ý: zip trả về tuples, nên cần ép kiểu về list nếu đề yêu cầu list of lists mutable
    # Dòng lệnh dưới đây tạo ra bản copy mới (không strictly O(1) space)
    new_matrix = [list(row) for row in zip(*matrix[::-1])]
    
    # Để force update vào biến matrix ban đầu (In-place ảo):
    matrix[:] = new_matrix

# Ví dụ chạy thử
matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]
rotate_pythonic(matrix)
print("Kết quả Pythonic:")
for row in matrix:
    print(row)

Lưu ý quan trọng: Cách dùng zip này tạo ra các object tuple mới trong bộ nhớ, nên về mặt lý thuyết nó tiêu tốn O(N^2) space tạm thời. Nếu đề bài “Hardcore” về bộ nhớ, hãy dùng Giải pháp 1.

5. Biến thể 

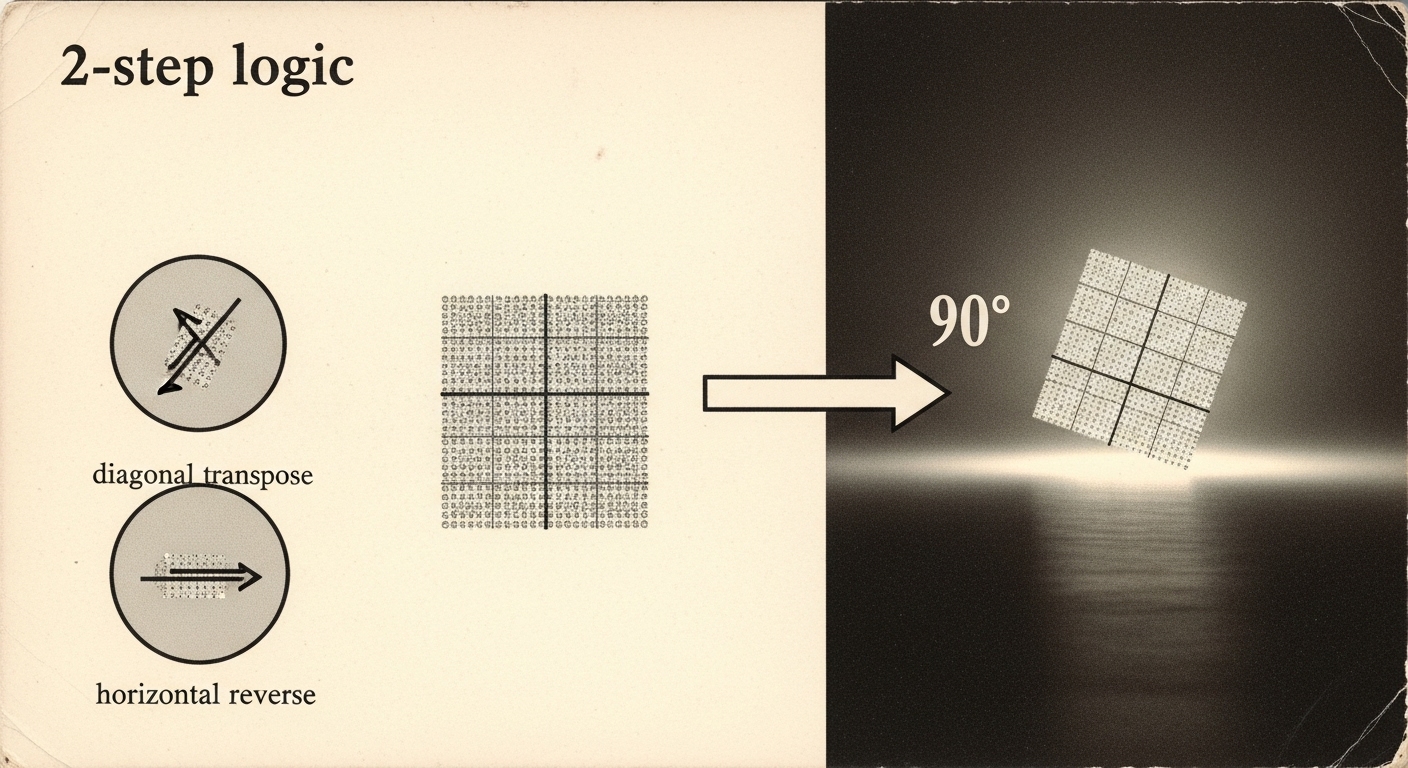
Biến thể 1: Xoay ngược chiều kim đồng hồ (90 độ trái)

Thay vì xoay phải, ta xoay trái.

Logic:

1. Transpose ma trận (như cũ).

2. Reverse Columns (Thay vì Reverse Rows). Hoặc đơn giản hơn: Reverse Rows trước, sau đó Transpose.

   Code: matrix[:] = [list(row) for row in zip(*matrix)][::-1]

Biến thể 2: Xoay 180 độ

Xoay 90 độ 2 lần.

Logic:

1. Reverse Rows (Đảo ngược thứ tự các hàng: Hàng 0 => Hàng N-1).

2. Reverse Elements in Row (Đảo ngược từng hàng).

   Tương đương: matrix.reverse() sau đó row.reverse() cho mỗi hàng.

6. Lỗi thường gặp

7. FAQ: Câu hỏi thường gặp

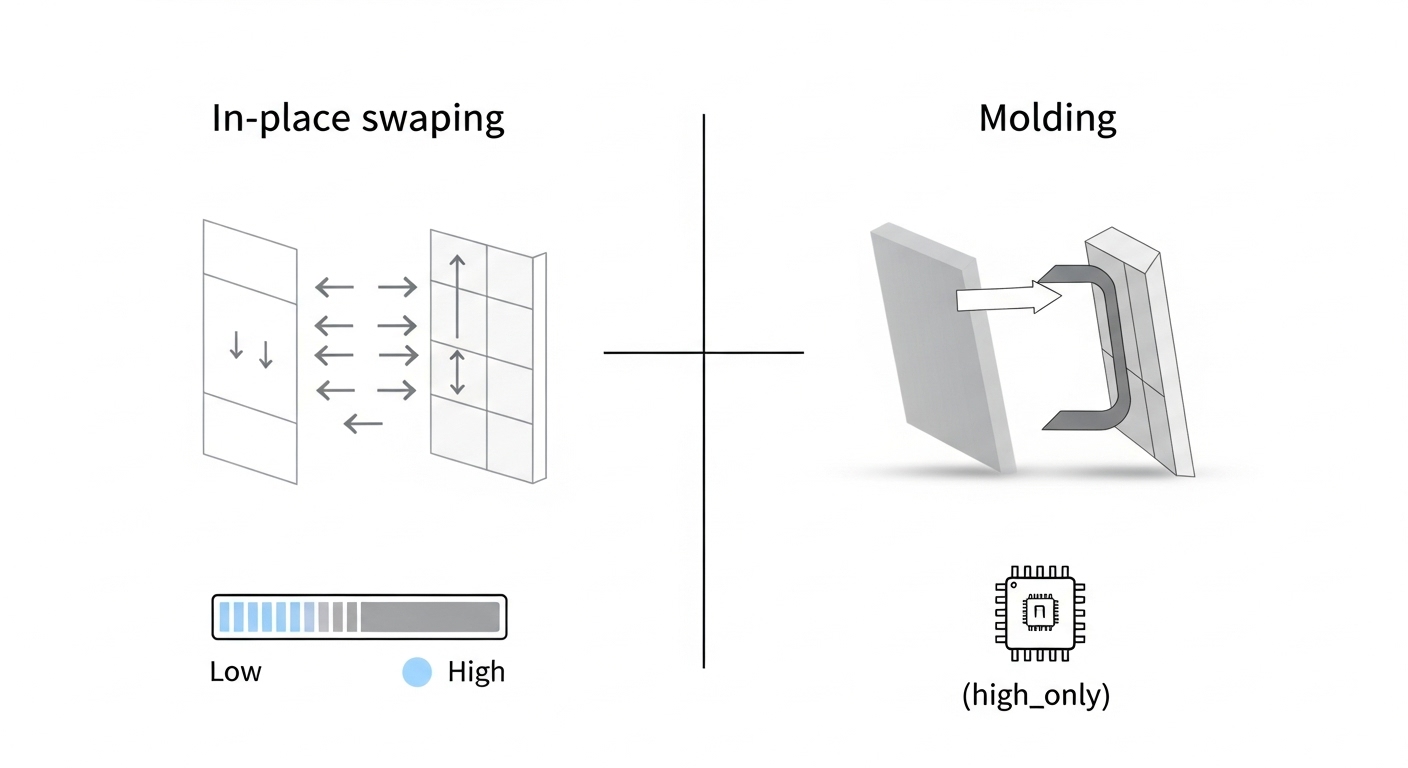
1. Tại sao cách Pythonic dùng zip lại tốn bộ nhớ?

Hàm zip trong Python 3 trả về iterator (tiết kiệm bộ nhớ), nhưng để xây dựng lại ma trận hoàn chỉnh [list(...)], ta buộc phải tạo ra các list mới chứa dữ liệu đã xoay, do đó tốn O(N^2) không gian tạm.

2. Bài này có thể giải bằng cách xoay từng lớp (Onion layers) không?

Có. Bạn có thể di chuyển 4 phần tử ở 4 cạnh cùng lúc (temp = top, top = left, left = bottom…). Cách này đạt chuẩn O(1) space tuyệt đối nhưng code rất phức tạp và dễ sai index. Cách Transpose + Reverse được ưa chuộng hơn vì dễ nhớ.

3. Ma trận không vuông (M x N) có xoay được không?

Được, nhưng không thể “In-place” hoàn toàn vì kích thước hàng/cột thay đổi (M x N => N x M). Bạn bắt buộc phải tạo ma trận mới.

8. Học tiếp gì sau bài này? 

Bài toán xoay ma trận là tiền đề cho các thao tác xử lý ảnh (Image Processing) cơ bản.

Để nâng cao kỹ năng xử lý mảng 2 chiều python, bạn nên làm tiếp:

1. Spiral Matrix: Duyệt ma trận theo hình xoắn ốc (Rất hay hỏi).

2. Set Matrix Zeroes: Tư duy đánh dấu trạng thái trên ma trận.

3. Search a 2D Matrix: Tìm kiếm nhị phân trên ma trận.

Các khóa học liên quan: 

• Làm chủ Python trong 4 tuần

• Học python căn bản thông qua lập trình 1 game

• Python Excel cho người đi làm

• Học lập trình Python cho mọi lứa tuổi

• Thành thạo xử lý dữ liệu với Python

• Tập làm kĩ sư Amazon vận hành robot nông nghiệp với Python

Một số sản phẩm từ Python:

• Tool MMO: “Máy xay clip” chuẩn MMO cho TikTok, YouTube Shorts, Facebook Reels

Một số sách lập trình Python bạn hãy tham khảo

• Tiki: Python
• Shopee: Pyhon