
-
Bài toán “xoắn ốc” là bài test tư duy quản lý chỉ số (index) kinh điển của Google, Microsoft.
-
Rèn luyện kỹ năng kiểm soát biên (Boundary Checks) để tránh lỗi IndexOutOfBound.
-
Bạn sẽ nắm được phương pháp “Bóc vỏ hành” (Layer-by-layer) để giải mọi bài toán duyệt ma trận phức tạp.
Tóm tắt nội dung
-
Nguyên lý duyệt theo 4 hướng: Phải => Xuống => Trái => Lên.
-
Kỹ thuật sử dụng 4 biến biên (
top,bottom,left,right). -
Xử lý các trường hợp ma trận không vuông (dễ bị in trùng lặp).
-
Code Python tối ưu Time & Space.
Bạn xem thêm:
- Giải Thuật Sudoku: Chiến Lược Backtracking Trong Python
- Hướng Dẫn Cài Đặt Python và PyCharm Chi Tiết: Tránh 5 Lỗi Sai Người Mới Hay Gặp
- 9 Bước Học Lập Trình Giao Diện Python Với tkinter: Xây Dựng Máy Tính Đơn Giản
1. Đề bài

Tên bài: Spiral Matrix (Ma trận xoắn ốc).
Đề bài:
Cho một ma trận kích thước MxN. Hãy trả về tất cả các phần tử của ma trận theo thứ tự xoắn ốc bắt đầu từ góc trên bên trái, đi theo chiều kim đồng hồ vào tâm.
Input:
-
Dòng đầu: Hai số nguyên M, N (số hàng, số cột).
-
M dòng tiếp theo: Mỗi dòng chứa N số nguyên.
Output:
-
Một dòng duy nhất chứa các phần tử theo thứ tự xoắn ốc, cách nhau bởi khoảng trắng.
Constraints:
-
1 <=M, N <=100.
-
-100 <= matrix[i][j] <=100.
Ví dụ 1:
Input:
3 3
1 2 3
4 5 6
7 8 9
Output:
1 2 3 6 9 8 7 4 5
Ví dụ 2 (Ma trận chữ nhật):
Input:
3 4
1 2 3 4
5 6 7 8
9 10 11 12
Output:
1 2 3 4 8 12 11 10 9 5 6 7
2. Phân tích tư duy
Để in xoắn ốc, hãy tưởng tượng chúng ta đang “bóc vỏ” ma trận từng lớp một từ ngoài vào trong.
Chúng ta cần 4 biến để giới hạn phạm vi chưa duyệt:
-
top: Chỉ số hàng trên cùng (bắt đầu = 0). -
bottom: Chỉ số hàng dưới cùng (bắt đầu = M-1). -
left: Chỉ số cột trái nhất (bắt đầu = 0). -
right: Chỉ số cột phải nhất (bắt đầu = N-1).
Logic Step-by-Step:
Quy trình lặp lại liên tục cho đến khi các biên gặp nhau:
-
Trái sang Phải: Duyệt hàng
toptừleftđếnright. Sau đó tăngtoplên 1 (để loại bỏ hàng vừa duyệt). -
Trên xuống Dưới: Duyệt cột
righttừtopđếnbottom. Sau đó giảmrightđi 1. -
Phải sang Trái: Duyệt hàng
bottomtừrightvềleft. Sau đó giảmbottomđi 1.-
Lưu ý: Phải kiểm tra nếu
top <= bottommới làm bước này (tránh trường hợp hàng đó đã bị duyệt ở bước 1).
-
-
Dưới lên Trên: Duyệt cột
lefttừbottomvềtop. Sau đó tăngleftlên 1.-
Lưu ý: Phải kiểm tra nếu
left <= rightmới làm bước này.
-
Bẫy thường gặp:
-
Ma trận 1 dòng hoặc 1 cột: Nếu không kiểm tra điều kiện kỹ ở bước 3 và 4, code sẽ in lặp lại các phần tử đã duyệt.
-
Hết phần tử giữa chừng: Vòng lặp phải dừng ngay khi tổng số phần tử in ra bằng MxN.
3. Giải pháp 1: Simulation
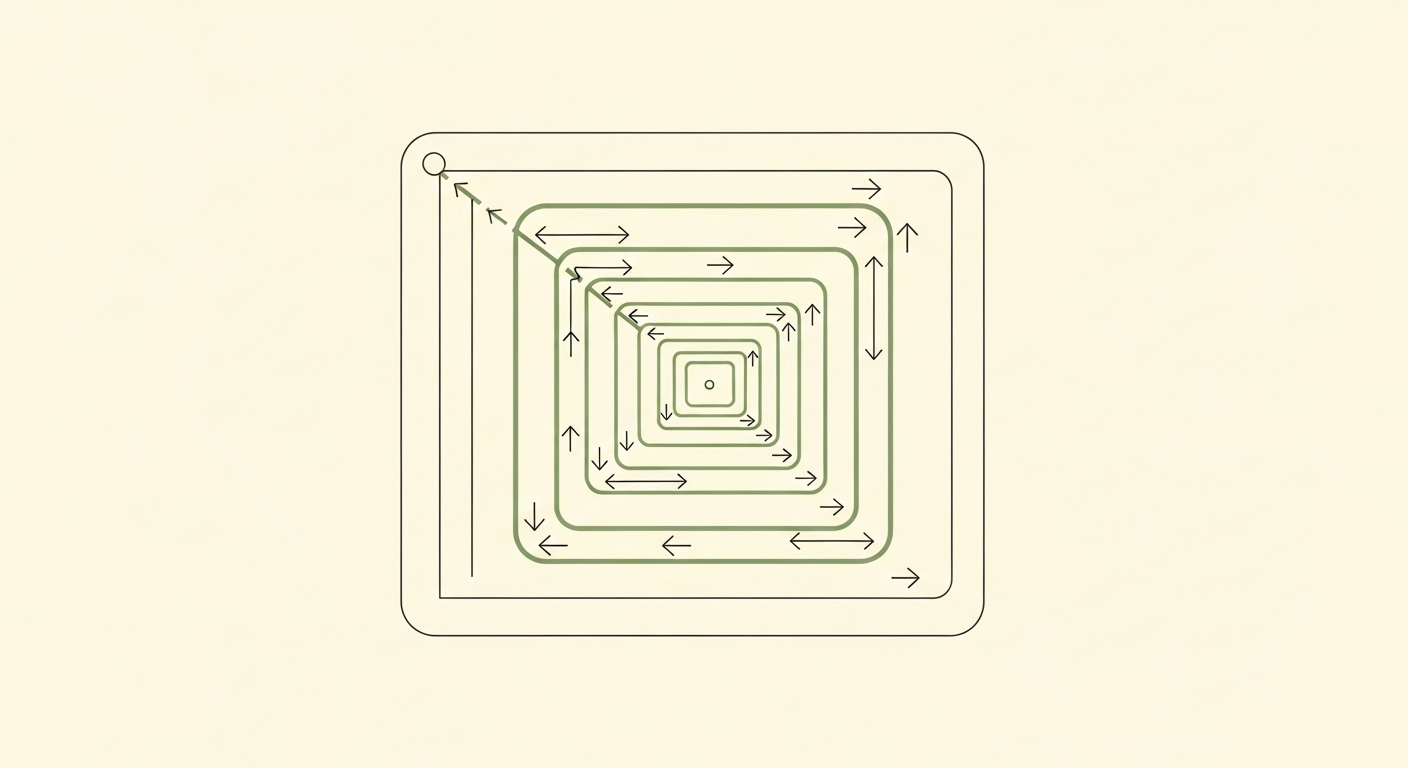
Cách này mô phỏng chuyển động của con rắn. Khi gặp biên hoặc ô đã đi rồi (seen), rắn sẽ rẽ phải.
Ý tưởng:
-
Mảng
dr(direction row) vàdc(direction col) để điều hướng: [0, 1, 0, -1] và [1, 0, -1, 0] tương ứng (Phải, Xuống, Trái, Lên). -
Dùng mảng phụ
seenkích thước MxN để đánh dấu ô đã đi.
import sys
def spiral_order_simulation(matrix):
if not matrix:
return []
R, C = len(matrix), len(matrix[0])
seen = [[False] * C for _ in range(R)]
ans = []
# Các hướng: Phải, Xuống, Trái, Lên
dr = [0, 1, 0, -1]
dc = [1, 0, -1, 0]
r = 0, c = 0
di = 0 # direction index (0->3)
for _ in range(R * C):
ans.append(matrix[r][c])
seen[r][c] = True
# Tính bước tiếp theo
cr, cc = r + dr[di], c + dc[di]
# Kiểm tra nếu bước tiếp theo hợp lệ và chưa đi
if 0 <= cr < R and 0 <= cc < C and not seen[cr][cc]:
r, c = cr, cc
else:
# Đổi hướng (xoay 90 độ)
di = (di + 1) % 4
r, c = r + dr[di], c + dc[di]
return ans
# Code chạy thử nhanh
# matrix = [[1,2,3],[4,5,6],[7,8,9]]
# print(spiral_order_simulation(matrix))
Phân tích Big-O:
-
Time Complexity: O(M x N) – Thăm mỗi ô đúng 1 lần.
-
Space Complexity: O(M x N) – Do dùng mảng
seenđể đánh dấu.
4. Giải pháp 2: Tối ưu Layer-by-Layer
Đây là cách tối ưu nhất về bộ nhớ, thường được mong đợi. Chúng ta chỉ dùng các biến biên (boundaries) thay vì mảng seen.
Code Python (Full Runnable)
import sys
def spiral_order_optimized(matrix):
result = []
if not matrix:
return result
# Khởi tạo 4 biên
top, bottom = 0, len(matrix) - 1
left, right = 0, len(matrix[0]) - 1
while top <= bottom and left <= right:
# 1. Quét từ Trái sang Phải (trên hàng top)
for i in range(left, right + 1):
result.append(matrix[top][i])
top += 1 # Thu hẹp biên trên
# 2. Quét từ Trên xuống Dưới (trên cột right)
for i in range(top, bottom + 1):
result.append(matrix[i][right])
right -= 1 # Thu hẹp biên phải
# --- Kiểm tra điều kiện ngắt quan trọng ---
if top > bottom or left > right:
break
# 3. Quét từ Phải sang Trái (trên hàng bottom)
for i in range(right, left - 1, -1):
result.append(matrix[bottom][i])
bottom -= 1 # Thu hẹp biên dưới
# 4. Quét từ Dưới lên Trên (trên cột left)
for i in range(bottom, top - 1, -1):
result.append(matrix[i][left])
left += 1 # Thu hẹp biên trái
return result
# --- Phần đọc Input chuẩn ---
def solve():
input_data = sys.stdin.read().split()
if not input_data:
return
iterator = iter(input_data)
try:
M = int(next(iterator))
N = int(next(iterator))
matrix = []
for _ in range(M):
row = []
for _ in range(N):
row.append(int(next(iterator)))
matrix.append(row)
result = spiral_order_optimized(matrix)
print(*(result)) # In ra các phần tử cách nhau bởi khoảng trắng
except StopIteration:
pass
if __name__ == "__main__":
solve()
Phân tích Big-O:
-
Time Complexity: O(M xN). Chúng ta duyệt qua toàn bộ phần tử của ma trận.
-
Space Complexity: O(1). Chúng ta chỉ lưu kết quả đầu ra, không dùng thêm bộ nhớ phụ nào đáng kể (trừ output array).
5. Biến thể nâng cao & Mở rộng
Biến thể 1: Tạo ma trận xoắn ốc
Đề bài: Cho số nguyên n, hãy tạo ra một ma trận vuông n x n chứa các số từ 1 đến n^2 theo hình xoắn ốc.
Hướng giải:
-
Logic y hệt Giải pháp 2.
-
Thay vì
result.append(matrix[i][j])(đọc), ta gánmatrix[i][j] = count(ghi). -
Tăng biến
countlên sau mỗi lần gán.
Biến thể 2: Xoắn ốc ngược
Đề bài: Bắt đầu từ toạ độ (rStart, cStart) bên trong, đi xoắn ốc ra ngoài.
Hướng giải:
-
Số bước đi sẽ tăng dần theo quy luật: 1 bước Phải, 1 bước Xuống, 2 bước Trái, 2 bước Lên, 3 bước Phải…
-
Dùng vòng lặp kiểm tra độ dài bước đi (
step_len) tăng dần sau mỗi 2 lần đổi hướng.
6. Lỗi thường gặp
| Lỗi sai | Tại sao? | Cách sửa |
| In trùng phần tử | Khi top == bottom (chỉ còn 1 hàng), vòng lặp bước 3 sẽ chạy ngược lại hàng vừa in ở bước 1. |
Thêm check if top <= bottom trước bước 3 và if left <= right trước bước 4. |
| Range Python | Quên rằng range(start, end) không bao gồm end. |
Luôn dùng range(left, right + 1) để lấy cả phần tử cuối. |
| Nhầm lẫn i, j | Nhầm lẫn giữa chỉ số hàng (row) và cột (col) trong các vòng for. | Quy ước rõ: Hàng thay đổi thì loop cột, Cột thay đổi thì loop hàng. |
7. FAQ: Câu hỏi thường gặp
1. Có cách nào viết ngắn gọn hơn không? (Pythonic Way)
Có một thủ thuật “Pop & Rotate” rất nổi tiếng:
def spiral(matrix):
res = []
while matrix:
res += matrix.pop(0) # Lấy hàng đầu
matrix = list(zip(*matrix))[::-1] # Xoay phần còn lại 90 độ ngược chiều
return res
Tuy nhiên: Cách này có độ phức tạp cao do việc tạo list mới liên tục, không nên dùng cho matrix quá lớn hoặc trong phỏng vấn yêu cầu tối ưu bộ nhớ.
2. Làm sao giải quyết nếu yêu cầu in ngược chiều kim đồng hồ?
Chỉ cần thay đổi thứ tự duyệt: (Xuống => Phải => Lên => Trái) và điều chỉnh các biến biên tương ứng.
3. Bài này dùng Đệ quy (Recursion) được không?
Được. Hàm đệ quy sẽ in viền ngoài (top, right, bottom, left), sau đó gọi đệ quy với top+1, bottom-1, left+1, right-1. Tuy nhiên, vòng lặp (Iterative) vẫn tốt hơn về mặt bộ nhớ Stack.
8. Học tiếp gì sau bài này?
Làm chủ ma trận xoắn ốc giúp bạn tự tin xử lý mọi bài toán duyệt mảng 2 chiều phức tạp.
Bài tập tiếp theo để nâng trình xử lý ma trận:
-
Spiral Matrix II: Tự tay điền số (Construct matrix).
-
Diagonal Traverse: Duyệt ma trận theo đường chéo zíc-zắc.
-
Game of Life: Mô phỏng tế bào trên lưới (cần xử lý 8 ô xung quanh).
Các khóa học liên quan:
Một số sản phẩm từ Python:
Một số sách lập trình Python bạn hãy tham khảo