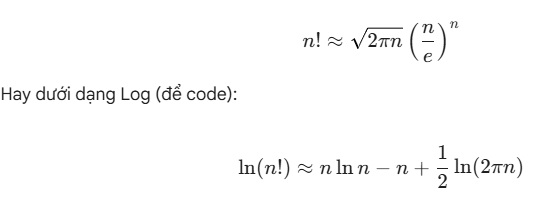“Giai thừa của 21 là bao nhiêu?” – Nếu bạn hỏi một lập trình viên C++ hoặc Java=> họ sẽ toát mồ hôi hột.
Tại sao? Vì 21! tương đương 5.1 x 10^19, vượt quá giới hạn của unsigned long long (64-bit integer). Kết quả sẽ bị tràn số (Overflow) và ra một con số âm hoặc rác rưởi.
Nhưng Python thì cười khẩy. Bạn gõ math.factorial(10000), Python trả về kết quả đúng ngay lập tức.
Điều này tạo ra một ảo tưởng nguy hiểm.
Lập trình viên Python thường chủ quan: “Python lo hết rồi, số to mấy cũng chơi”.
Kết quả: Vào năm 2022, Python đã phải tung ra bản vá khẩn cấp (CVE-2020-10735) vì hacker có thể làm sập server chỉ bằng việc gửi một yêu cầu tính giai thừa hoặc lũy thừa số lớn, rồi ép server chuyển nó sang chuỗi (str()).
Bài viết này không dạy bạn tính toán. Bài viết này dạy bạn kiểm soát con quái vật “Số Nguyên Lớn” (Big Integer) để xây dựng hệ thống tài chính/bảo mật an toàn tuyệt đối.
Bạn xem thêm:
- Bài tập Python: Kiểm Tra Năm Nhuận
- Bài Tập Python: In Bảng Cửu Chương
- Bài tập Python: In Dãy Số Từ 1 Đến N
1. Cấp độ 1:
Trước khi viết code, hãy nhìn vào “nội tạng” của Python.
1.1. Tại sao Python không bao giờ bị tràn số?
Trong C, số nguyên là một ô nhớ cố định (4 bytes hoặc 8 bytes).
Trong Python, số nguyên (int) là một Object phức tạp (PyLongObject).
Nó hoạt động như một mảng động (dynamic array).
-
Nếu số nhỏ: Dùng 1 “digit” (30-bit).
-
Nếu số lớn (n!): Python tự động nối thêm các “digit” mới vào mảng.
-> Giới hạn duy nhất là RAM của bạn.
1.2. Cái giá phải trả (Trade-off)
Việc tính toán trên mảng động chậm hơn tính toán trên CPU Register khoảng 10-100 lần.
Khi bạn tính 100.000!, Python phải thực hiện thuật toán nhân số lớn (như thuật toán Karatsuba) chứ không phải phép nhân CPU đơn thuần.
2. Cấp độ 2: Tư duy thuật toán
Ẩn dụ: Xếp chồng đĩa
Mỗi lần bạn gọi hàm đệ quy factorial(n), máy tính phải lấy một cái đĩa (Stack Frame) đặt lên chồng đĩa để lưu trạng thái hiện tại (biến n đang bằng bao nhiêu).
-
factorial(10): 10 cái đĩa. OK. -
factorial(5000): 5000 cái đĩa. Chồng đĩa đổ sập. -> Stack Overflow.
Trong Python, giới hạn mặc định là 1000 (để bảo vệ máy). Bạn có thể tăng bằng sys.setrecursionlimit, nhưng đó là cách làm của kẻ liều mạng. Khi Stack quá lớn, nó lấn sang bộ nhớ Heap, gây crash hệ điều hành.
Code “Hello World” (Nhưng đã được tối ưu)
import math
import sys
# Khắc phục lỗi bảo mật Int-to-String (Python 3.11+)
# Cho phép convert số có tối đa 100.000 chữ số (Default là 4300)
try:
sys.set_int_max_str_digits(100000)
except AttributeError:
pass # Python bản cũ chưa có tính năng này
def calculate_factorial_safe(n: int) -> int:
"""
Sử dụng Module C-Extension (math) thay vì viết lại vòng lặp.
Đây là cách nhanh nhất vì nó chạy ở tầng máy (Machine Code).
"""
if n < 0:
raise ValueError("Giai thừa không xác định cho số âm.")
return math.factorial(n)
3. Cấp độ 3:
Vấn đề thực tế của Freelancer: Khách hàng yêu cầu in kết quả 100.000! ra màn hình.
-
Tính toán: Mất 1 giây.
-
Chuyển sang chuỗi (String Conversion) để in: Mất 10 phút hoặc treo máy.
-
Nguyên nhân: Thuật toán chuyển đổi từ nhị phân (Binary) sang thập phân (Decimal) để hiển thị có độ phức tạp là O(N^2).
Giải pháp Architect: Scientific Notation & Logarithms
Thay vì in con số dài 500 trang giấy A4, hãy in dạng khoa học (1.23 x 10^500) hoặc độ lớn (Logarithm).
Source Code: The Smart Calculator
import math
import sys
import time
class SmartFactorial:
def __init__(self):
# Mở giới hạn string conversion an toàn
if hasattr(sys, "set_int_max_str_digits"):
sys.set_int_max_str_digits(50000)
def compute(self, n: int):
print(f"\n🚀 Đang tính {n}! ...")
# 1. Đo lường thời gian tính toán (Computation Time)
t0 = time.perf_counter()
result = math.factorial(n)
t1 = time.perf_counter()
calc_time = (t1 - t0) * 1000
# 2. Xử lý hiển thị thông minh (Smart Output)
# Nếu số quá lớn (> 1000 chữ số), KHÔNG convert sang string ngay
# Sử dụng Logarithm để tính độ dài
num_digits = int(math.log10(n) * n) if n > 0 else 1 # Ước lượng sơ bộ
if num_digits < 1000:
print(f"✅ Kết quả: {result}")
else:
# Chỉ tính toán độ dài chính xác bằng len(str()) nếu thực sự cần thiết
# Cảnh báo rủi ro I/O
print(f"⚠️ Kết quả có {len(str(result))} chữ số.")
print(f"ℹ️ Dạng khoa học: {self.format_scientific(result)}")
print(f"⚡ Core CPU Time: {calc_time:.4f} ms")
@staticmethod
def format_scientific(number):
"""Chuyển BigInt sang dạng a.bc x 10^n mà không cần convert toàn bộ chuỗi"""
# Đây là kỹ thuật trick: Lấy log10 để tìm số mũ
# log10(x) = exponent.mantissa
if number == 0: return "0"
# Với số cực lớn, không thể dùng math.log10 trực tiếp vì Overflow
# Ta dùng convert string giới hạn
s = str(number)
exponent = len(s) - 1
mantissa = s[:4] # Lấy 4 số đầu
return f"{mantissa[0]}.{mantissa[1:]}e+{exponent}"
if __name__ == "__main__":
tool = SmartFactorial()
tool.compute(100)
tool.compute(20000) # Thử thách số lớn
4. Cấp độ 4:
Đây là đẳng cấp cao nhất. Trong AI/Machine Learning (Natural Language Processing, Bioinformatics), chúng ta thường xuyên tính xác suất:
Kết quả của phép tính này thường siêu nhỏ (gần 0) hoặc siêu lớn.
Nếu dùng float, nó về 0 (Underflow).
Nếu dùng int, nó tràn RAM.
Giải pháp của Chuyên gia: Log-Space Arithmetic.
Thay vì tính A x B, ta tính ln(A) + ln(B).
Giai thừa trở thành tổng Log: ln(n!) = ln(1) + ln(2) + … + ln(n).
Hoặc xấp xỉ bằng Công thức Stirling.
Thuật toán xấp xỉ Stirling (Dành cho Big Data)
Source Code: High-Performance Math Service
import math
import decimal
class StatisticalEngine:
"""
Engine toán học dùng cho Machine Learning / Data Science.
Không bao giờ tính giá trị thực của n!.
Luôn làm việc trên không gian Logarithm (Log-Space).
"""
@staticmethod
def log_factorial(n: int) -> float:
"""
Tính ln(n!) cực nhanh.
Dùng math.lgamma (Log Gamma Function) - Được viết bằng C cực tối ưu.
Độ phức tạp O(1) hoặc O(log n) tùy implementation, nhanh hơn O(N) vòng lặp.
"""
# Gamma(n+1) = n!
return math.lgamma(n + 1)
@staticmethod
def stirling_approximation(n: int) -> float:
"""
Tính giá trị xấp xỉ cho n siêu lớn (n > 1 tỷ) mà math.factorial sẽ treo máy.
"""
if n == 0: return 0
# Công thức Stirling dạng Log
return n * math.log(n) - n + 0.5 * math.log(2 * math.pi * n)
@staticmethod
def calculate_combination_log(n: int, k: int) -> float:
"""
Tính C(n, k) = n! / (k! * (n-k)!)
Trong Log-space: log(C) = log(n!) - log(k!) - log(n-k)!
Tránh hoàn toàn việc tính số lớn.
"""
return math.lgamma(n+1) - math.lgamma(k+1) - math.lgamma(n-k+1)
# Demo ứng dụng: Tính xác suất trúng Vietlott (Chọn 6 số từ 45)
# C(45, 6)
engine = StatisticalEngine()
log_result = engine.calculate_combination_log(45, 6)
real_result = math.exp(log_result) # Convert ngược lại (chỉ khi số nhỏ)
print(f"Log xác suất: {log_result:.4f}")
print(f"Số cách chọn (approx): {real_result:,.0f}")
# Kết quả chuẩn xác: 8,145,060 mà không cần thực hiện phép nhân giai thừa nào!
Tại sao code này đáng giá $5000/tháng?
-
math.lgamma: Đây là vũ khí bí mật. Nó tính log giai thừa nhanh gấp tỷ lần vòng lặp. Đây là cách các thư viện nhưSciPy,TensorFlowhoạt động. -
Zero Overflow Risk: Không bao giờ tạo ra số nguyên lớn. Bộ nhớ luôn ổn định.
Các khóa học liên quan:
Một số sản phẩm từ Python:
Một số sách lập trình Python bạn hãy tham khảo