
-
Bạn đã giải được Sudoku 9×9, nhưng nếu đề bài yêu cầu 16×16, 25×25 hay 100×100 thì sao?
-
Nâng cấp tư duy từ “Hardcode” sang “Dynamic” (Tổng quát hóa vấn đề).
-
Một thuật toán duy nhất xử lý đúng cho mọi kích thước bảng N x N, miễn là đúng luật Sudoku.
Tóm tắt nội dung
-
Cách xác định kích thước vùng con (Block) dựa trên N.
-
Kiểm tra điều kiện tiên quyết: N có phải số chính phương?
-
Giải pháp tổng quát dùng Hashing.
-
Code Python xử lý Dynamic Input.
Bạn xem thêm:
- Giải Thuật Sudoku: Chiến Lược Backtracking Trong Python
- In ma trận xoắn ốc Python: Giải thuật & Code tối ưu
- 9 Bước Học Lập Trình Giao Diện Python Với tkinter: Xây Dựng Máy Tính Đơn Giản
1. Đề bài
Cho một bảng Sudoku kích thước N x N (N dòng, N cột). Hãy kiểm tra bảng này có hợp lệ không.
Biết rằng, một bảng Sudoku N x N hợp lệ phải thỏa mãn:
-
Bảng phải là hình vuông.
-
Kích thước N phải là một số chính phương (ví dụ: 4, 9, 16, 25…). Gọi k = sqrt(N) là kích thước của vùng con (block).
-
Mỗi hàng chứa các số từ 1 đến N, không trùng lặp.
-
Mỗi cột chứa các số từ 1 đến N, không trùng lặp.
-
Mỗi vùng con kích thước k x k chứa các số từ 1 đến N, không trùng lặp.
Input:
-
Dòng đầu: Số nguyên N.
-
N dòng tiếp theo: Mỗi dòng chứa N số nguyên.
Output:
-
YEShoặcNO.
Ví dụ 1 (4 x 4 – Hợp lệ):
Input:
4
1 2 3 4
3 4 1 2
2 1 4 3
4 3 2 1
Output:
YES
(Giải thích: N=4, kích thước vùng con là 2 x 2. Các vùng con là [1,2,3,4]… đều hợp lệ)
2. Phân tích tư duy Thuật Toán Kiểm Tra Sudoku
Sự khác biệt lớn nhất giữa bài 9×9 và bài N x N là cách chúng ta xác định tọa độ của vùng con (Sub-grid).
Logic toán học:
-
Số chính phương: Trước khi kiểm tra số, ta phải kiểm tra xem bảng có chia được thành các vùng đều nhau không.
-
N=9 => k=3 (Vùng 3 x 3). Hợp lệ.
-
N=16 => k=4$ (Vùng 4 x 4). Hợp lệ.
-
N=10 => k gần bằng 3.16. Không thể chia vùng Sudoku chuẩn. => Báo lỗi ngay.
-
-
Công thức Block Index:
Với bảng 9 x 9, ô (r, c) thuộc khối thứ:
(r // 3, c // 3).Với bảng N x N, đặt k = sqrt(N). Ô (r, c) thuộc khối thứ:
(r // k, c // k).
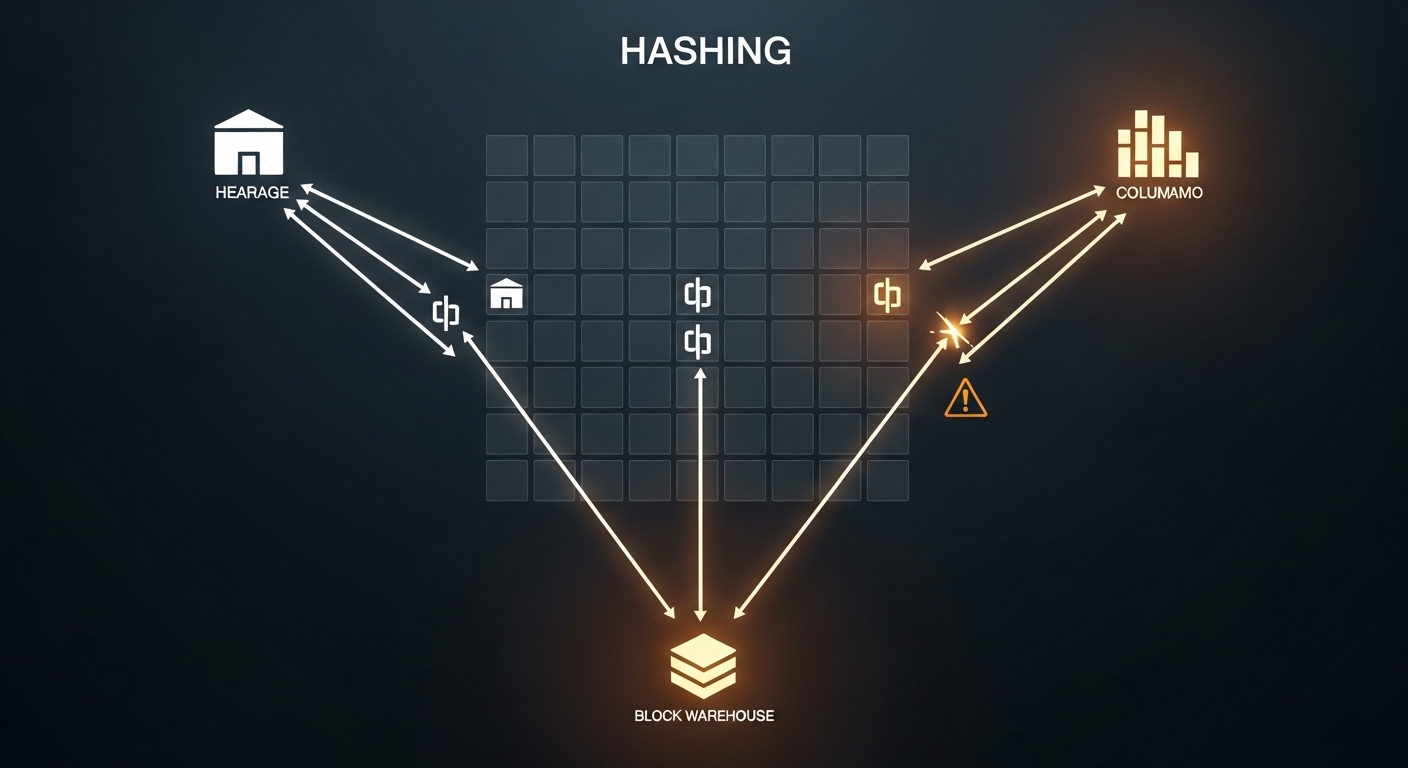
Chiến lược:
Chúng ta sẽ sử dụng phương pháp Hashing (One-pass) vì nó dễ mở rộng (scale) nhất cho các bài toán Dynamic Size. Thay vì viết 3 vòng lặp lồng nhau phức tạp, ta mã hóa vị trí vào Set.
3. Giải pháp
Đây là đoạn code “cân” được mọi kích thước, từ 4×4 đến 100×100.
Code Python
import sys
import math
def is_valid_sudoku_nxn(n, board):
# 1. Kiểm tra N có phải số chính phương không
k_float = math.sqrt(n)
k = int(k_float)
if k * k != n:
# Nếu N không phải số chính phương (ví dụ N=5, N=10),
# không tồn tại định nghĩa vùng con chuẩn.
return False
seen = set()
for r in range(n):
# Kiểm tra độ dài hàng (phòng trường hợp input thiếu/thừa)
if len(board[r]) != n:
return False
for c in range(n):
val = board[r][c]
# Kiểm tra giá trị phải nằm trong [1, N]
# (Lưu ý: Nếu đề cho phép số 0 là ô trống, sửa điều kiện này)
if val < 1 or val > n:
return False
# Logic Hashing định danh
# row_id: Đánh dấu số val đã xuất hiện ở hàng r
# col_id: Đánh dấu số val đã xuất hiện ở cột c
# box_id: Đánh dấu số val đã xuất hiện ở khối (r//k, c//k)
row_key = (0, r, val)
col_key = (1, c, val)
box_key = (2, r // k, c // k, val)
if row_key in seen or col_key in seen or box_key in seen:
return False
seen.add(row_key)
seen.add(col_key)
seen.add(box_key)
return True
# --- Phần đọc Input Dynamic ---
def solve():
input_data = sys.stdin.read().split()
if not input_data:
return
iterator = iter(input_data)
try:
# Đọc N
n_str = next(iterator)
n = int(n_str)
board = []
for _ in range(n):
row = []
for _ in range(n):
val = int(next(iterator))
row.append(val)
board.append(row)
# Gọi hàm kiểm tra
if is_valid_sudoku_nxn(n, board):
print("YES")
else:
print("NO")
except StopIteration:
# Xử lý lỗi nếu input bị thiếu giữa chừng
print("NO")
except ValueError:
# Xử lý lỗi nếu input không phải số
print("NO")
if __name__ == "__main__":
solve()
Phân tích Big-O:
-
Time Complexity: O(N^2).
-
Ta duyệt qua mỗi ô của bảng đúng 1 lần.
-
Các thao tác
addvàchecktrong Set tốn O(1) trung bình. -
Tổng thời gian tỷ lệ thuận với tổng số ô (N x N).
-
-
Space Complexity: O(N^2).
-
Trong trường hợp tệ nhất (bảng điền kín và hợp lệ), tập
seensẽ chứa 3 x N^2 phần tử (mỗi ô đóng góp 3 key).
-
4. Biến thể
Biến thể 1: Mini-Sudoku (4×4, 6×6)
-
4×4: Block là 2 x 2. Rất phổ biến cho người mới tập chơi.
-
6×6 (Jigsaw/Irregular): Đôi khi Block là hình chữ nhật 2 x 3.
-
Cách sửa code: Input thêm kích thước Block (ví dụ
block_rows,block_cols). Công thức key đổi thành(2, r // block_rows, c // block_cols, val).
-
Biến thể 2: Hexadoku (16×16)
-
Dùng các ký tự
0-9vàA-F(hoặc1-16). -
Cách sửa code: Nếu input là ký tự (A, B…), cần có hàm mapping chuyển
A-> 10,B-> 11… trước khi đưa vào logic chính.
5. Lỗi thường gặp
| Lỗi sai | Tại sao? | Cách sửa |
| Quên tính $k$ | Dùng cứng // 3 cho bảng 16×16 sẽ sai bét block. |
Luôn tính $k = int(\sqrt{N})$. |
| Input thiếu dòng | Đọc input không kiểm tra len(board). |
Thêm check len(row) != n và len(board) != n. |
| Tuple Key conflict | Dùng key string dễ trùng nếu nối chuỗi ẩu (VD: “1” + “1” => “11”). | Dùng Tuple (type, index, value) là an toàn nhất và nhanh nhất. |
6. FAQ: Câu hỏi thường gặp
1. Làm sao để kiểm tra N có phải số chính phương nhanh nhất?
Trong Python, cách đơn giản nhất là:
k = int(math.isqrt(n)) # Python 3.8+
return k * k == n
2. Nếu N rất lớn (VD: N=1000) thì Set có bị tràn bộ nhớ không?
Với N=1000, tổng ô là 1.000.000. Set chứa 3 triệu phần tử. Python xử lý tốt việc này (tốn khoảng vài trăm MB RAM). Nếu cần tiết kiệm hơn, có thể dùng Bitmasking (nếu N nhỏ) hoặc mảng boolean visited[3][N][N+1] (nếu bộ nhớ cấp phát tĩnh rẻ hơn Dynamic Hash Set).
3. Tại sao không dùng List lồng nhau để kiểm tra?
Dùng List để check in (x in list) tốn $O(N)$. Tổng thuật toán sẽ thành O(N^3). Với N lớn, N^3 là thảm họa về hiệu năng. Set (O(1) lookup) là bắt buộc.
7. Học tiếp gì sau bài này?
Bạn đã có công cụ để kiểm tra tính đúng đắn của mọi bảng Sudoku. Bước tiếp theo:
-
Sudoku Solver NxN: Nâng cấp thuật toán Backtracking ở bài trước để giải bảng 16×16 (Gợi ý: Cần tối ưu cực mạnh bằng “Dancing Links” hoặc Heuristics vì Backtracking thường quá chậm với N=16).
-
Valid Sudoku Irregular (Jigsaw): Vùng con không phải hình vuông mà là hình ziczac bất kỳ (được định nghĩa bằng 1 ma trận map vùng).
Các khóa học liên quan:
Một số sản phẩm từ Python:
Một số sách lập trình Python bạn hãy tham khảo